Ever watched a black hole launch matter into space? Me neither, but this simulation comes pretty close!
The video below is a visualization of a high resolution 2D simulation of the accretion disk of a black hole, made by me using the state-of-the-art GRMHD* code called HAMR** on a single GPU. The simulations are partly refined to give an effective resolution of 600×600 pixels. Units are in terms of Rg (gravitational radius), so the simulation applies to any black hole mass. The accretion disk starts out with a poloidal magnetic flux, which powers the jet once the accretion starts.
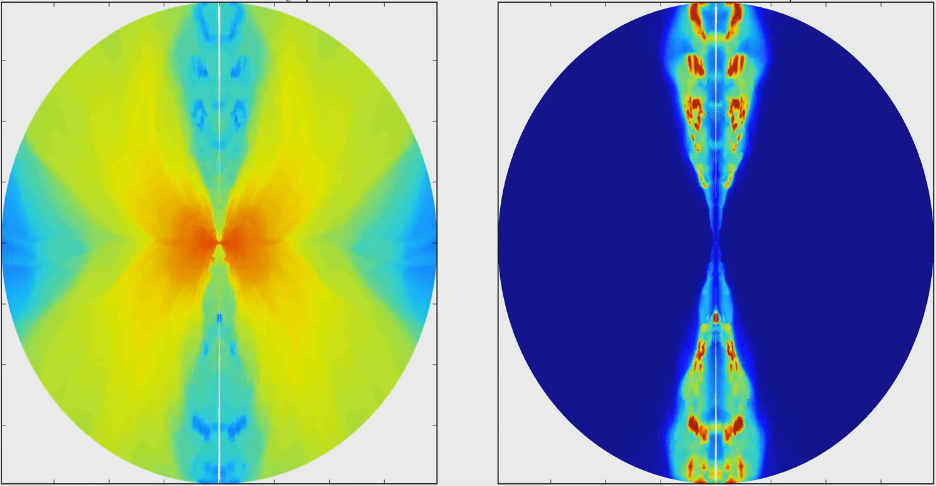
The left plot shows the density distribution, clearly visualizing the accretion disk itself (accretion onto the black hole starts around 600 R_g/c). The right plot shows the velocity of the material in terms of the Lorentz factor, visualizing the astrophysical jet. We get this for free once we set up the disk!
My Learning process
For my Master thesis I’ve been learning from and working together with Matthew Liska. He is a PhD at the University of Amsterdam and used to be a Master student in Sera’s group (like me now). My project is directed at one of the amazing things we can study with his code HAMR**: relativistic jets in 3D. Although still in development, HAMR is the fastest code of its kind (GRMHD) on the planet by far because it’s optimized in multiple ways. That makes the learning process challenging and exciting at the same time. HAMR was developed based on the open source code HARM2D, which is freely available with tutorials right here.
Future directions
HAMR allows us to study jets in 3D simulations, with disks that are tilted with respect to the spin of their host black hole. My goal is to analyze how the wobbling of the disk affects the behavior of the jet. We are able to extend our simulations towards unprecedented scales (10,000 or even 100,000 Rg) to study how the jets travel into outer space. An example will follow soon!
*GRMHD stands for General Relativistic Magnetohydrodynamics.
**HAMR stands for Harm2d with Adaptive Mesh Refinement. Credits due to Matthew Liska and Alexander Tchekhovskoy.