Hi there! I’m Koushik, a 2nd year PhD student in Sera’s group. I did my undergrad in India, a really beautiful country and also known to lay quite a lot of emphasis on highly theoretical research work (might even be a tad too much!). While I did my masters in Physics and my thesis on Einstein’s theory of general relativity (GR in short), my interests lie with applications to astrophysical phenomena, e.g. black holes.
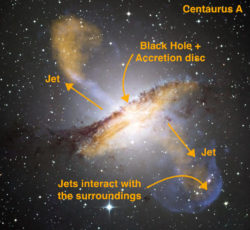
Description: Colour composite image of Centaurus A, revealing the lobes and jets emanating from the active galaxy’s central black hole. Credit: ESO/WFI (Optical); MPIfR/ESO/APEX/A.Weiss et al. (Submillimetre); NASA/CXC/CfA/R.Kraft et al. (X-ray)
The most extreme sources of gravity are black holes lying deep in the heart of galaxies, millions to billions of times the mass of the Sun, such as Sagittarius A* in the Milky Way (our own galaxy). Here gravity interacts intricately with plasma material (like ionised gas, much like the content of the Sun), which have their own magnetic fields, creating astonishing structures such as jetted outflows.
My task is to understand some of these interactions in jets and create simulations to replicate what we see in nature. How do we do that? Well, we use theories about fluid dynamics, add a pinch of magnetic fields and set our equations in a mathematical framework dictated by general relativity. This entire set of equations is known as General Relativistic Magneto-Hydro Dynamics or GRMHD. Starting from a basic setup of a torus of gas embedded with magnetic fields (called an accretion disc) around a rotating central black hole, we can self consistently make simulations of jets propagating over parsec scales. Just contemplating about the sizes and scales of these structures can boggle the mind. Just imagine, 1 parsec is about 30 trillion kilometres! Quite a distance, don’t you think? Probably would need a lot of fuel to travel that far.
Jets and Energy transfers
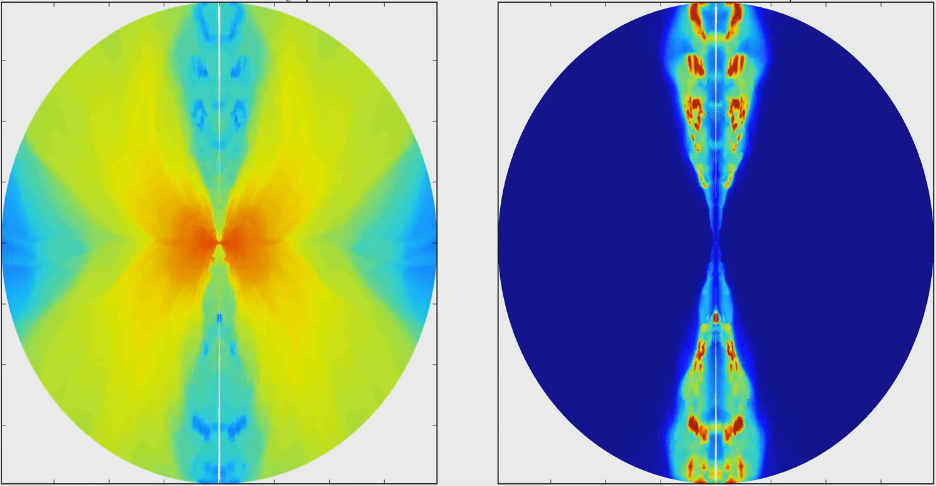
Using long time period observations, astronomers can actually map out individual features which travel as part of the jet and calculate their propagation velocity. Some of these features were found to travel with superluminal speeds, or in order words, “relativistically” (e.g. See Biretta et al. 1999). Thus, jets contain particles travelling at near light speed, which may be possible by converting the available magnetic energy to kinetic form (Blandford & Rees 1974) and has been shown to work via simulations (Komissarov 2007, Tchekhovskoy et al. 2008). But that is not the whole story. I have found, similar to previous work, that the acceleration of jets is also highly dependent on its structure or shape. In this movie (Link to youtube movie), I show 2 dimensional slices of two simulations. Imagine you have a horizontal torus and cut out a cross section vertically through the centre of the torus. What we are left with are two egg shaped images of the disc. In the movie, the left side shows a small disc (shown in grayscale) and the right one a large disc. I show the jet in terms of Lorentz factor in colour. The term “Lorentz factor” is a function of velocity and is used in describing velocity magnitudes in relativistic physics.
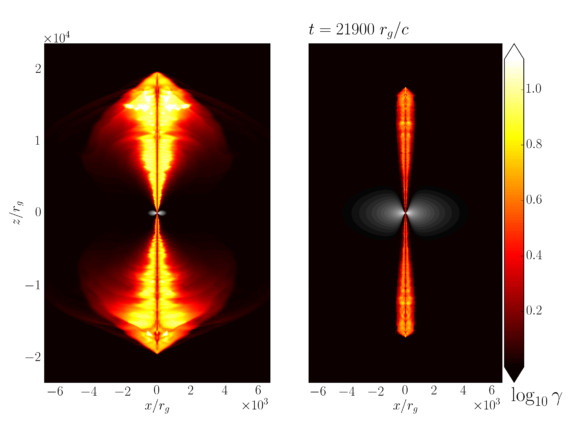
As the movie starts, we see the black hole (black spot in the middle) begins to eat matter falling in from the disc and soon, a jet is launched. From the snapshot, we can see that left jet is really wide and fast, forming a giant cocoon-like structure when it interacts with the surrounding medium. Looks really similar to the image of Centaurus A, doesn’t it? By the way, the right one also looks similar to another “famous” jet- the M87 jet. So, jets that are allowed to spread out and become huge usually have higher velocities, while jets that are forced to collimate and remain “slim” are slower.
But why? It looks very contradictory to what we observe for a flow in a pipe. The smaller the diameter of the pipe, faster is the speed of the water flowing through it, right? Well, that is true for non-magnetic flows. When you add magnetic fields in fluid propagation, everything you have learned about water and pipes go out the window! The trick here is the extra Lorentz force exerted by the magnetic field on the jet. This is where magnetic energy gets converted to kinetic. The transverse gradient of the magnetic field must vary such that magnetic field lines undergo differential bunching. Therefore, acceleration does not depend on uniform lateral expansion or contraction, but on the non-uniformity of the lateral movement of field lines (Tchekhovskoy et al. 2009). This explains why rapidly expanding jet regions accelerate more.
Grasping just this piece of information gives us a unique insight on how much different magneto-hydrodynamics (M-HD) is from only “HD”. Add to this interaction with the disc and the surrounding medium, and you got a massively complex system with energy conversions between magnetic, thermal and kinetic forms occurring all around. But that’s a story for another day!