Hi, readers. I am Doosoo Yoon, who recently has joined Sera’s group. Since I started my academic career in astronomy, I have strongly interested in performing numerical simulations to figure out how astrophysical phenomena can be interpreted. In my first post, I would like to briefly talk about some basic processes of computational astrophysics and mindset for building a Matrix-world, from several articles I’ve read.
Conducting research with numerical simulation requires three main components: understanding of dominant physical processes for the problem of interest, programming them with numerical algorithms and utilizing maximum capabilities of the computers for the simulations (Elmegreen 2011). In fact, all theoretical equations need to be approximated, depending on the subject. There is no single equation that describes all physical phenomena in the universe. For example, Newton’s equation explains gravity accurately only when the speed of the object is far slower than the speed of light and the object is not located at the strong gravity field (e.g. nearby a black hole). Also, in most astrophysical studies, the gaseous medium is treated as fluid, but only macroscopic nature is computed with Navier-Stokes equations.
Besides the theoretical equations, problems in astrophysics are often rendered tractable by concentrating on the specific scale (length, time, velocity) of interest (Heing 2014). Even with the state-of-art supercomputers, it is not feasible to cover all scale ranges of the universe in a single simulation. The projects with a large-scale cosmological simulation focus on understanding the shape of the universe, which is observed by all-sky surveys, however, these studies are difficult to tell us how the individual galaxy evolves in detail. On the contrary, the small-scale numerical studies, such as jet formation, stellar evolution, focus on understanding of the nature of the target object, but they are often difficult to address the effects of the source on its environment. However, indeed these numerical studies in the different scales are complementary to each other.
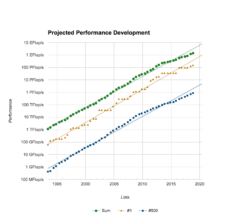
For the last several decades, the speed and power of computers have been growing exponentially, with an improvement by a factor of two roughly every 1.2 years. In Figure 1, the y-axis indicates the growth of computing capability for the fastest modern supercomputer (see middle triangles) as a function of the year (e.g. the unit PFlop/s indicates the 10^12 floating point operations per second). This shows that the modern revolution in computing enables us to extend our knowledge, solving more complicated problems. One interesting fact is that the smartphone that most people use every day is quite more powerful than the computer that was used to bring the first astronauts to the Moon in the Apollo mission back to 1960s.
Coding an astrophysical problem-set may like establishing a Matrix-world. We hope our Matrix-word would be flawless and operated perfectly that no one inside it chooses a blue pill and causes a trouble. However, this is always not the case. Practically we are used to facing many challenges, which lead us to get out of line. All the time, we need to be ready for suspecting if the assumptions we made are okay for our problem and if numerical artifact comes into play.
With this numerical tool, to date, my research has focused on the dynamical evolution of energetic outflows (e.g. wind or jet) from a black hole or a neutron star, and their interactions with the surrounding medium. Also, the interplay between the active galactic nuclei feedback from a central supermassive black hole and its host galaxy is of great interest to me. As I join Sera’s group, I am excited to have a chance to study what is really going on near the black hole, regarding with an accretion, a wind, and a jet.



