There’s no doubt about it: Einstein’s general theory of relativity has changed the way we understand the cosmos, with its crowning glory being the discovery of black holes. Last year (2019), in May, I gave a short talk about the Event Horizon Telescope results on a webinar (link here) hosted by SPACE- India, an organization dedicated to bringing the wonders of space to school children in India. You can see the pdf of the talk here. I had a fun time interacting with them and (hopefully!) answered some of the questions from these curious young minds. I, of course, thank SPACE-India for the opportunity to reach so many kids. It was an awesome experience!

For me, it was fascinating to learn that, as far back as in 1783, Jon Michell, following the footsteps of Isaac Newton, envisioned a scenario where a celestial object could become so massive that the velocity required to escape its gravitational pull may become larger than the speed of light. Would light become trapped then? You can quickly spot that a black hole, essentially, displays the same behavior! Of course, it wasn’t easy, but, in 1915, Karl Schwarzschild pushed the theory of general relativity to the limit and found a solution to Einstein’s field equations for the gravitational field of a spherically symmetric object in vacuum, or what came to be later known as a static (or non-rotating) black hole (see here for the solution). Further progress came in the form of the Kerr solution applicable for a rotating black hole in empty space.
The webinar brought back memories of my master’s thesis project, which was on solving Einstein’s field equations in a planar and non-planar geometry accounting for a scalar field. This scalar field is representative of a chargeless particle, for example, a photon, which makes my solutions an analog of the Casimir effect – a phenomenon that accounts for forces arising due to a quantized field, such as a photon field or even a quantum gravitational field. Interestingly, I found that solutions for these set of equations that indicated that a test particle in such a gravitational field might spring out of a singularity, similar to the concept of a “white hole” which, as you might guess, behaves in exactly the opposite way a black hole does – a white hole shoots out photons! It was indeed amazing to see these solutions appear out of nowhere. What was even more amazing was the realization that general relativity is such a moldable construct! This flexibility, over the years, has triggered a barrage of interesting solutions such as the wormhole, e.g., Schwarzschild wormhole, Einstein – Rosen bridges. A wormhole is a passage from one point of the universe to the other (a cool device for intergalactic travel in space fiction, such as Star Trek), and requires the presence of a mystical material called “exotic matter”.
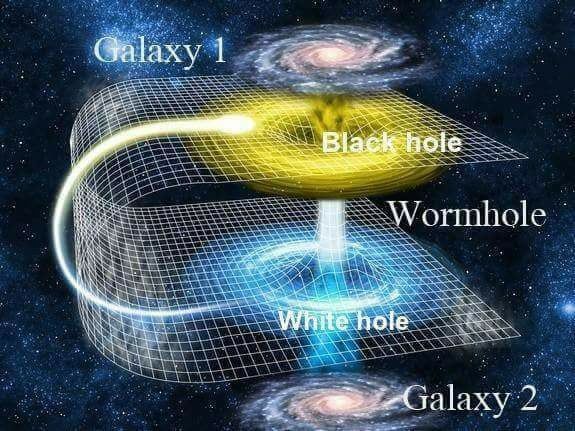
It was quite surprising that during the webinar, most of the questions I got was whether the Event Horizon Telescope saw a wormhole in M87! I guess it just goes to show that the next generation of astronomers has lofty ambitions and high expectations of our observing and theoretical capabilities! Excellent for the future, don’t you think?