In part I we showed that space and time coordinates lead to different types of interval, spacelike and timelike respectively. Hence if we are given a line element expression in terms of any coordinates, we can figure out which of the coordinates are spatial and temporal, by looking at the sign of their coefficients. The coordinate t is temporal not because of the variable used, but the timelike interval it creates. Now we may ask: if a coordinate is spatial or temporal, does it always keep this identity?
The short answer is, no. More rigorously, it depends on the structure of spacetime. For flat spacetime as shown in the last part, all the coefficients in the line element are constant, so the spatial/temporal coordinates remain spatial/temporal at any point in spacetime. However, in more general cases, the coefficients are functions of the coordinates. For instance, we can express the flat spacetime line element in terms of spherical coordinates:

Here the coefficients of the coordinates θ and ϕ are no longer constant, but they remain non-negative throughout space, and thus these two coordinates are always spatial.
What happens if spacetime is curved? Let’s consider the spacetime around a non-rotating black hole, with the line element taking the following form:

where rS is the Schwarzschild radius. At this radius, the coefficient of the radial term diverges, marking the event horizon of the black hole. The horizon separates the spacetime into two regions with distinct properties.
In the outer region (r > rS), the coefficient 1 – rS/r is positive, so the dt2 term remains negative and the dr2 term remains positive. There is nothing special, though the scaling on coordinates differs from flat spacetime. Once we cross the horizon into the inner region (r < rS), the coefficient 1 – rS/r flips to negative, and everything becomes unusual: the dt2 term turns positive while the dr2 term turns negative. In other words, time is spacelike and space is timelike! What does this mean physically?
Since the spacetime interval of a massive object is always timelike, to keep the interval negative, now dr must be non-zero. Therefore, in the inner region of the black hole, the radial coordinate becomes unidirectional that can only decrease (because objects entering from outside have initial dr < 0): anything within the horizon is predestined to hit the singularity at the centre. Death is doomed with no escape. On the other hand, surprisingly we can have dt = 0! The time coordinate is no longer forced to change monotonically, so we are allowed to move to the past/future, or even stay at rest in time! Well, of course before hitting the singularity.
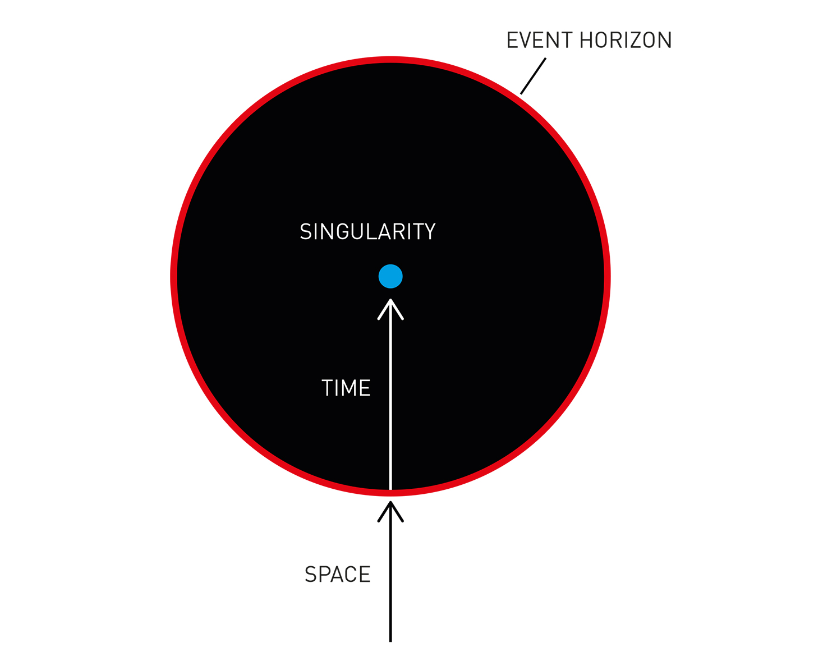
Now we’re aware how devastating black holes are, as they can make space and time swap their roles, with the original spatial/temporal coordinate becoming temporal/spatial in the black hole interior. This is the case of a non-rotating black hole, what about a rotating one? We’ll meet features even more amazing in part III.