Can black holes make spaghetti? Like Obama, black holes would reply ‘Yes we can’! To top that off they can make spaghetti out of anything – using their ‘gravitational machinery’. In this three part series we will see how black holes employ gravity to do so! Before we go exploring black hole’s ‘spaghetti skills’, in part I, first let us look closer to home, at our very own Earth’s ‘spaghetti skills’ and its connection to the concept of tidal forces.
Gravity and Tidal Force
Let’s begin with the familiar. Earth produces a gravitational field by the virtue of its mass, and objects immersed in this field feel a gravitational force. Objects far away from the earth (like astronauts in space) feel little to no gravity. Thus Earth’s gravity (and gravity of any other object) is strongest near it and decreases as one moves away. This implies that there is a gradient in the gravitational field, i.e., the strength of the field decreases the further away we are from the object.
A tidal force arises because of the presence of such a gradient. If an extended body (something which is not a point object) is present in a gravitational field it will notice that due to its spatial extent, different parts of this body experience a different gravitational force. As the name ‘tidal’ force suggests they are what causes the ocean tides.
Now let’s explore what tidal forces can do.
Stretching

Imagine a metallic cylindrical rod of length L. Let this rod’s center be situation at distance R from the Earth’s center (in addition let’s also assume we are far away from the Earth’s surface) and it be oriented so that one end of the rod (end A) is closer to the Earth (see Fig. 1 for an illustrative sketch). Gravity is stronger at the end closer to the Earth than the end which further away (end B) resulting in end A being pulled more than end B. As a result, the rod experiences a stretching force which tends to elongate the rod.
I have chosen to depict the forces on the extremities of the rod to illustrate the basic idea of tidal forces. However, the tidal force acts across the entire length of the rod. The reader can imagine the rod to be composed of several segments. As each segment is located at a different distance from Earth, each segment will experience a different force and thus, a different acceleration.
[ Paragraphs in white boxes (like this current one) will contain mathematical expressions for people who want to get an idea of how to calculate tidal forces / acceleration]. This post has been written so that readers interested only in the big picture and less in the mathematical details can still read and understand the post. For those who want the math – don’t skip the white boxes; those not interested in the math – just skip them.
We can derive the formula for the magnitude of tidal acceleration for the two ends of the rod by calculating the acceleration at either end and then subtracting them –
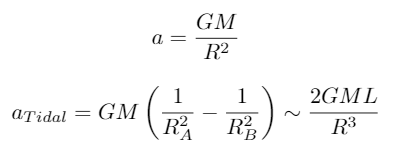
In the formula above: G is the gravitational constant, M is the mass of the Earth, and L is the length of the rod. For instructive purposes, let’s calculate the tidal acceleration of a rod which is, 2 meters = 200 cm long. Let’s say the rod is located at the Earth’s surface for ease of calculation. This gives us the tidal acceleration as 0.0006 cm/sec2. Compared to acceleration due to gravity (980 cm/sec2) this number is quite small (1.6 million times smaller)!
The tidal stretching forces are a million times smaller at the Earth’s surface as compared to Earth’s gravity! No wonder we don’t feel stretched all the time!
Summarizing: Gravity can stretch objects. Stay tuned for Part II, where we will see how gravity squeezes objects!




