It is widely believed that the luminosities of M87 and Sagittarius A*, which are the major targets of the Event Horizon Telescope collaboration, are significantly lower than their Eddington luminosities. It means that the mass accretion rates of these objects are so low that the material accreting onto the central supermassive black hole can be interpreted as the radiatively inefficient accretion flow (RIAF), which is geometrically thick and optically thin (See “disk thin / thick?!” for the disk models). In such a (geometrically) thick disk, it is generally acceptable to assume that the interactions between ions and electrons are very poor, so they are not in thermal equilibrium, resulting in the different temperatures between them.
To compute the radiative properties (e.g., synthetic images at a certain frequency, spectral energy density distribution) from general relativistic magnetohydrodynamic (GRMHD) simulations, many researchers make use of general-relativistic ray-tracing as post-processing (see “general-relativistic radiative transfer codes”). If the simulation is carried out by single-fluid GRMHD runs, which evolve the fluid as a single element (ions + electrons), the following question is how we can input the electron temperature to the ray-tracing algorithms, which is likely different from the gas temperature that is obtained from the simulations.
The general way to handle this is adopting the prescription of the temperature ratio between ions and electrons. The simplest prescription is the constant ratio (Ti / Te ~ constant) regardless of any physical properties at each location. This simple treatment has been developed by the physical motivation that the temperature ratio should be different in each region (i.e., jet and disk region). Moscibrodzka et al. (2016) introduced a simple formula, the so-called “R-beta” prescription, in which the temperature ratio depends on the local magnetization, and Anantua et al. (2020) suggested several other formulae, in which the prescription is parameterized as a function of the magnetic pressure and gas pressure.
It is really challenging to find reasonable parameters for the electron temperature model from a single GRMHD simulation. Therefore, many studies employ the prescription with a range of parameter space and provide a best-bet model by comparing the observed emission. As presented above, ions and electrons are not in thermal equilibrium for the case of the low accretion rate, it is also not clear if such temperature ratio is well-saturated value or not.
As a complementary approach, many theoretical astrophysicists make use of micro-scale simulations such as particle-in-cell (PIC) runs, in which multi-species elements evolve by kinetic interactions (see “PIC methods in astrophysics”). These PIC simulations provide great knowledge in inferring the interplay between ions and electrons, but cannot cover the region of interest as large as the global GRMHD can cover. Instead, the results from PIC simulations help us to build some approximated formula that can be applied to the global simulations.
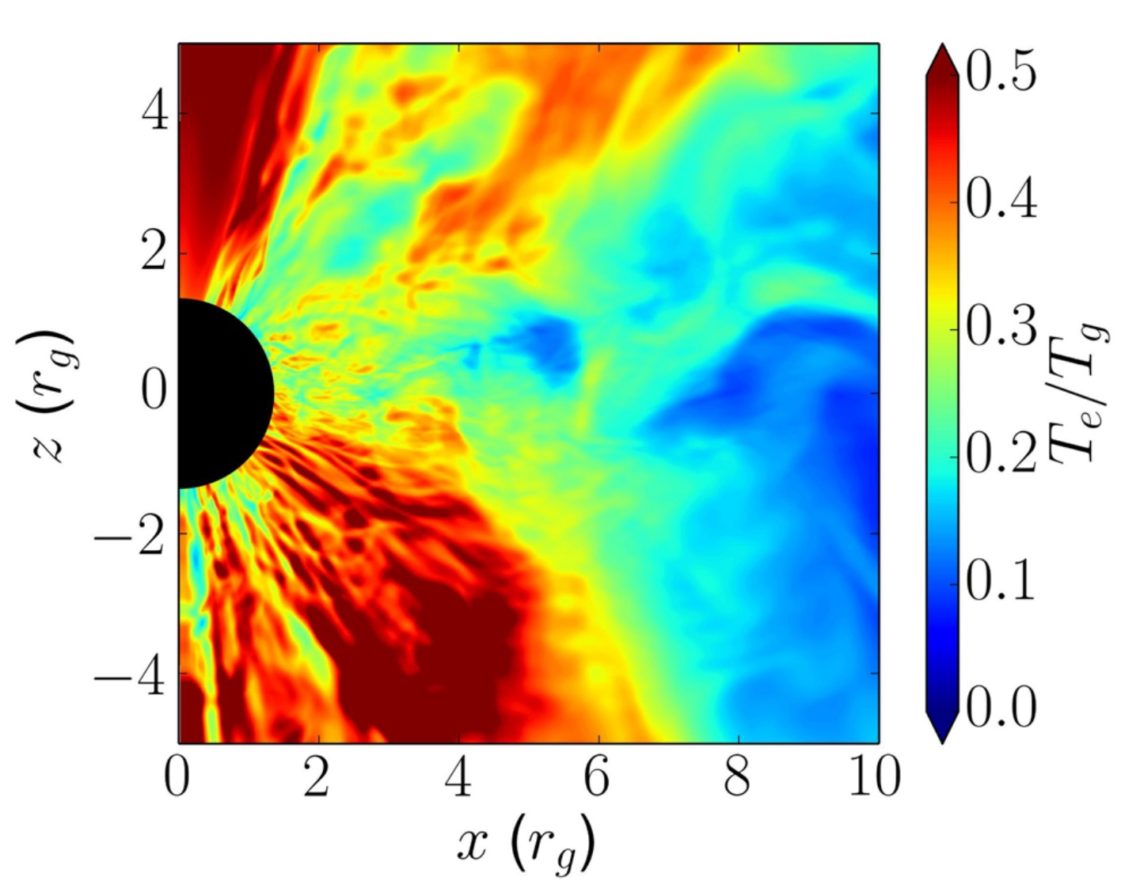
To overcome the drawback of the electron temperature prescription in calculating the radiative properties from a single fluid GRMHD simulations, recently two-Temperature GRMHD simulations have been developed in which electron temperature and ion temperature evolve independently (see Fig 1.). The main GRMHD code that our group has developed in the collaboration with the group in Northwestern University (Prof. Alexander Tchekhovskoy) and Harvard University (Drs. Matthew Liska and Koushik Chatterjee), H-AMR, also recently has equipped the two-temperature gear. Our H-AMR family will be able to present interesting results from these advanced two-Temperature GRMHD simulations, so stay tuned.