In this blog, I will introduce the mathematical concept of wormholes in general relativity, the possible implications in serious astrophysical research, and how this became an inspiration for the german science fiction series: Dark.

With mathematics, it is possible to duplicate the geometry of spacetime, for example, we can make a copy of the Schwarzschild geometry (describing a static Black Hole) in reverse. In this reversed version, the copy behaves as a White Hole where all objects are destined to escape from it, contrary to the case of a black hole. In Fig. 2, if we consider region I being the universe where we live, then by traveling to the future we reach region II (black hole) and can never return once we enter the event horizon, or by following a past line we reach region III (white hole) a part of spacetime from which things can escape to us, while we can never get there.
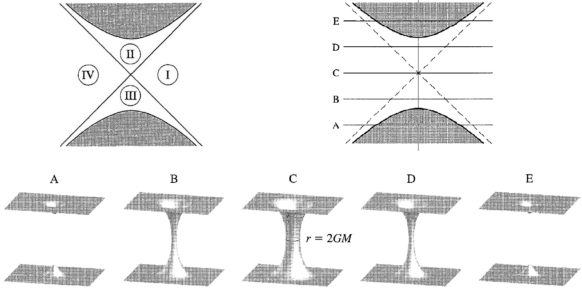
Meanwhile, region IV cannot be reached from our region I either forward or backward in time, this is a mirror image of ours. It can be thought of as being connected to region I by a wormhole, the Einstein-Rosen bridge (neck-like configuration joining two distinct regions) useful to give a “reasonable” explanation to time travel in Dark.
However, considering the spacelike slices A-E (from past to future), the Schwarzschild geometry describes two regions (A) that reach toward each other, join together via a wormhole for a while (B-D), and then disconnect (E). The wormhole closes up too quickly for our heroes Jonas Kahnwald and Martha Nielsen to cross it from one region into the next. The Einstein-Rosen bridge made of a black hole and a white hole, cannot be crossed!

Fortunately for our curiosity there exist other geometries of wormholes whose properties are more advantageous, like being crossable both ways (without any sort of horizons), stable in time, and with not too strong gravitational “forces” (generated by its geometry) so they don’t damage us or the spaceship. The simplest example is the nonspinning, traversable Morris-Thorne wormhole that contains no horizon, no singularities, and is stable, where the spacetime contains negative energy conditions that are forbidden in General Relativity but can be mathematically possible in quantum field theory or string theory.
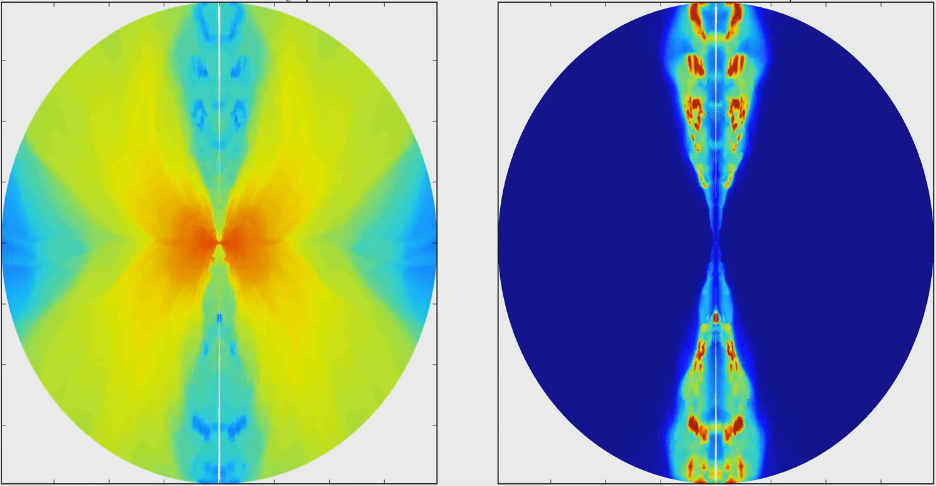
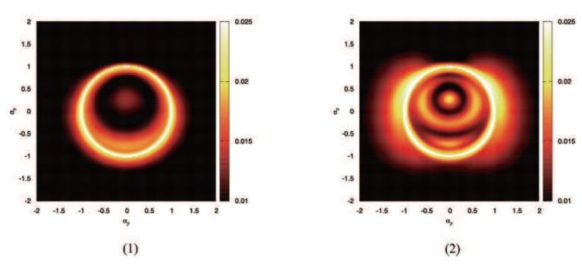
Despite the previous mathematical move, motivated by the symmetry of equations, is artificial and cannot be backed up by any sort of physical observation, this type of wormhole is interesting to astrophysical researchers because light rays are also deviated by this geometry and the images of the wormhole surrounded by dust are distorted, as shown in Fig. 4 for the case of the Ellis wormhole. On the left panel, a bright ring appears in the image, similar to the first image of the M87 supermassive black hole. On the right panel, there appears a weakly luminous pattern due to the existence of entities on the other side region of the wormhole, because light can also go through! Therefore, astrophysicists can tell the difference between the shadow of a “real” (Kerr) black hole and a mimicker such as the Morris-Thorne or Ellis wormhole, all we need in future observations is higher resolution and sensitivity for our telescopes.
The takeaway message for the writers of Sci-fi movies and series is to better use Morris-Thorne wormhole geometry instead of the Einstein-Rosen bridge, as the first seems to meet all the necessary conditions for intergalactic and time travel that even science researchers study them seriously.