With the advent of the Christmas time, it is common to put yourself a nice candle in the living room (or sometimes even four or more). It is particularly nice to enjoy the warm and dim orange light, softly flickering and creating a cozy atmosphere.
As an astrophysicist researching the light emission from outflows moving at almost the speed of light towards us, I was wondering what would happen to such a Christmas candle if I would do the same thing to the candle – move it at the speed of light.
Clearly, the airstream would blow out the candle and it wouldn’t burn if we put it into a vacuum, so let’s instead rather think of the candle as a simplified representation for a light source. Let’s for simplicity ignore the shape of the flame and approximate it as a point-like source, for example as if we had a very large living room and the candle would be far away. Let’s say that it is emitting isotropically at rest, i.e. shining with the same brightness into every direction. And let’s for simplicity also assume the candle emits light only at a single orange wavelength and that it is flickering with a typical duration between the bright moments.
How would that change for a candle that would move it at the 99% of the speed of light? Three things would be different compared to the candle at rest: It’s color would become more blueish, it would flicker faster, and it would become brighter!
The change of color and the faster flickering can be understood by the same arguments: We can think of the emitted light as a wave of electromagnetic fields that travels at the speed of light. The waves consist of swings from maximum to minimum to maximum and so on. We can think of a flat water surface and constantly tipping with the finger on the surface, with the water perturbation representing a maximum of the electromagnetic field. Then the case of the candle corresponds to tipping constantly at the same position, and the observer sitting at a distance observing the perturbations arriving at the same frequency as the emitted tipping of the surface (see the orange candle in figure 1). However, as a soon as the candle/emitter moves at a speed comparable to the wave speed, they will move almost as far as the perturbation (water wave or light) travelled before the next tipping, leading to a smaller time between two maxima for the observer, i.e. a higher frequency (see the blue candle in figure 1). This is also known as the Doppler effect and famous for sound waves where it changes the perceived sound frequency of an ambulance moving towards you, compared to when it moves away from you. In the same way we can also understand how the frequency of light – which is nothing else but its color – changes towards higher frequencies – from orange via yellow to green to blue – when the candle moves towards us.
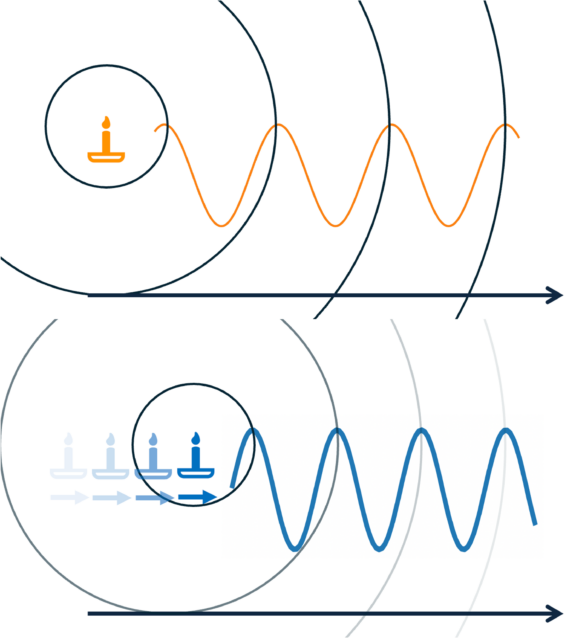
While the frequency of the electromagnetic field waves is extremely short (about 500 000 000 000 000 maxima per second), the flickering can be seen as a much slower modulation of the overall amplitude of that signal (for example 1 second between two flickerings). Thus again, if the emitting “candle” keeps up significantly with the emitted signals, then also for this time span between two maxima, an observer at rest would see a much shorter time between two flickering pulses compared to a candle at rest.
The last effect on the relativistic Christmas candle is the fact that the emission is beamed into a forward cone, i.e. the isotropic emission of the candle is perceived more like a flashlight pointing in the direction of its motion. This is a result of the underlying assumption of special relativity that the speed of light is the same for every observer with arbitrary relative motion. To achieve this even for observers moving close to the speed of light, the perceived space and time get deformed accordingly, such that the speed of the emitted light remains constant. This leads to an effective focusing towards the direction of motion of the candle, as shown in figure 2, and a brighter appearance to an observer at rest.
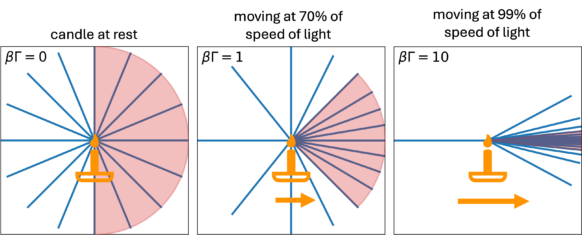
To wrap it together: If we spiced up our Christmas atmosphere in our extremely large living room by a candle moving at relativistic speeds (i.e. close to the speed of light) towards us, the candle would appear (1) blue-shifted and (2) faster flickering due to the compression of the observed frequency when moving almost as fast as the speed of the light waves, and also (3) the candle would brighten up due to the beaming of the light into a small forward cone to preserve the speed of light to the same observed value for us.




