When you are asked to simulate the flow of gas in some corner of the universe, the first thing you need is a system of equations that govern the same. But let’s just say you have found yourself a closed, well posed system of equations, what next?
The next choice one has to make is the method by which to solve the found system of equations. There are two broad classes to the same: Eulerian and Lagrangian. With an Eulerian approach, you divide the region of space into smaller regions, a grid, and simulate transport over the grid over time, giving you snapshots of how the grid looks at a particular point in time. With a Lagrangian approach, you take the initial blob of gas you are simulating, divide them up into smaller blobs and see how these blobs interact with each other over time.
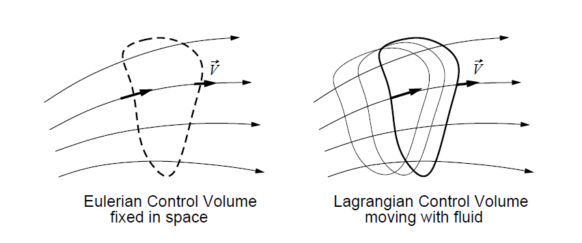
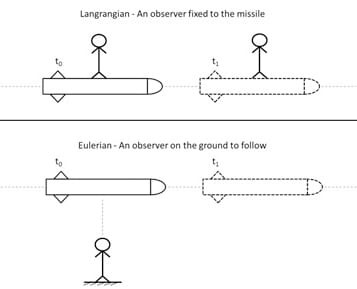
Let us visualize this. Imagine standing on the ground, one can sit on the missile at a specific patch of the sky and see a missile fly through and past it. This is essentially the Eulerian approach. The other perspective could be to sit on the missile as it passes through the sky, that is the Lagrangian approach.
This brings us to the question in the title, to mesh or not to mesh? If done the right way, physically it should not matter. However, to accurately evolve fluids in a Lagrangian manner, we must divide our blobs into many sub-blobs and then loop over each of these to update what they would look in the next timestep, this is very expensive considering the Eulerian alternative of looping over cells in space. However, for some problems, like particle transport, Eulerian just does not capture enough dynamics for the computational tradeoff. Another argument against Eulerian is also that the timestep is limited by how coarse my grid is, and that contributes to issues in the stability of the solution itself.

Most General-Relativistic Magnetohydrodynamic codes are based on Eulerian prescriptions (HAMR, BHAC, KHARMA, etc.), however Lagrangian alternatives exist (SPHINCS-BSSN). In my research direction, I break down my problem into smaller sub-problems, marked by different time and length scales to use both Lagrangian and Eulerian formalisms. In my future blog posts I aim to get into the Eulerian background and what goes into the choice of meshing in terms of coordinates systems and addressing stability. (Title picture credits: Flow illustrator)