Did you ever wonder if light can bounce off a charged particle like an electron? And how this interaction can lead to some of the highest-energy gamma-ray radiation that we have ever observed in the universe? In this double blog post, I will build up an intuitive and visual understanding of how this quantum billiards between light and charged particles works (part 1) and how its relativistic version can explain some of the most fascinating astrophysical ultra-high-energy observations (part 2).
Recently, the astrophysical community is flooded by exciting new observations from the Large High Altitude Air Shower Observatory (LHAASO) and High Altitude Water Cherenkov Experiment (HAWC). Both detectors are measuring light with frequencies in the range of 1-1000 trillion times larger than what our eye can see, called ultra-high-energy (UHE) gamma-rays – and the sky is brighter at these frequencies than expected. At these large frequencies, it is more helpful to think of light as a quantum particle called “photon” that carries energy (equivalent to its frequency), instead of the classical image of an electromagnetic wave. Obviously, the large number of new UHE detections also raises the question on how so many regions of our cosmic neighborhood can be so bright at these ultra-high energies, and this is precisely where the scattering of light and electrons comes in.
In order to understand the origin of such ultra-high-energy photons intuitively, it is crucial to first understand the seemingly opposite process, the scattering of light (or equivalently a photon) on an electron at rest, known as Thomson or Compton scattering. The apparent inverse Compton scattering – as the origin of the UHE photons – turns out to be just the same as “normal” Compton scattering in combination with basic relativistic effects.
Thomson scattering
One of the first people concerned about how a light wave can scatter off a resting electron was Joseph John Thomson in the early 1900s (hence the name). He thought of light as an electromagnetic wave that accelerated the charge to wiggle and thereby reflect the light, with the reflected intensity depending on the direction. In the photon particle interpretation, he derived what we call the cross section of this interaction, i.e. the probability that the photon gets scattered by the electron into a different direction, commonly described by the scattering angle between the scattered direction and the incoming direction. This scattering is illustrated in Fig. 1, where a light ray or photon (purple wiggly line) hits an electron at rest (central black dot). The left (right) panel shows the setup before (after) the scattering. What Thomson found, is that the probability of scattering is fairly uniform, but with a slight preference forward and backward (often referred to as the peanut shape that emerges when instead plotting the radius of the dot according to the probability). This is illustrated by the difference in intensity of dots on the sphere in the right panel, where each dot corresponds to the tip of many scatterings.
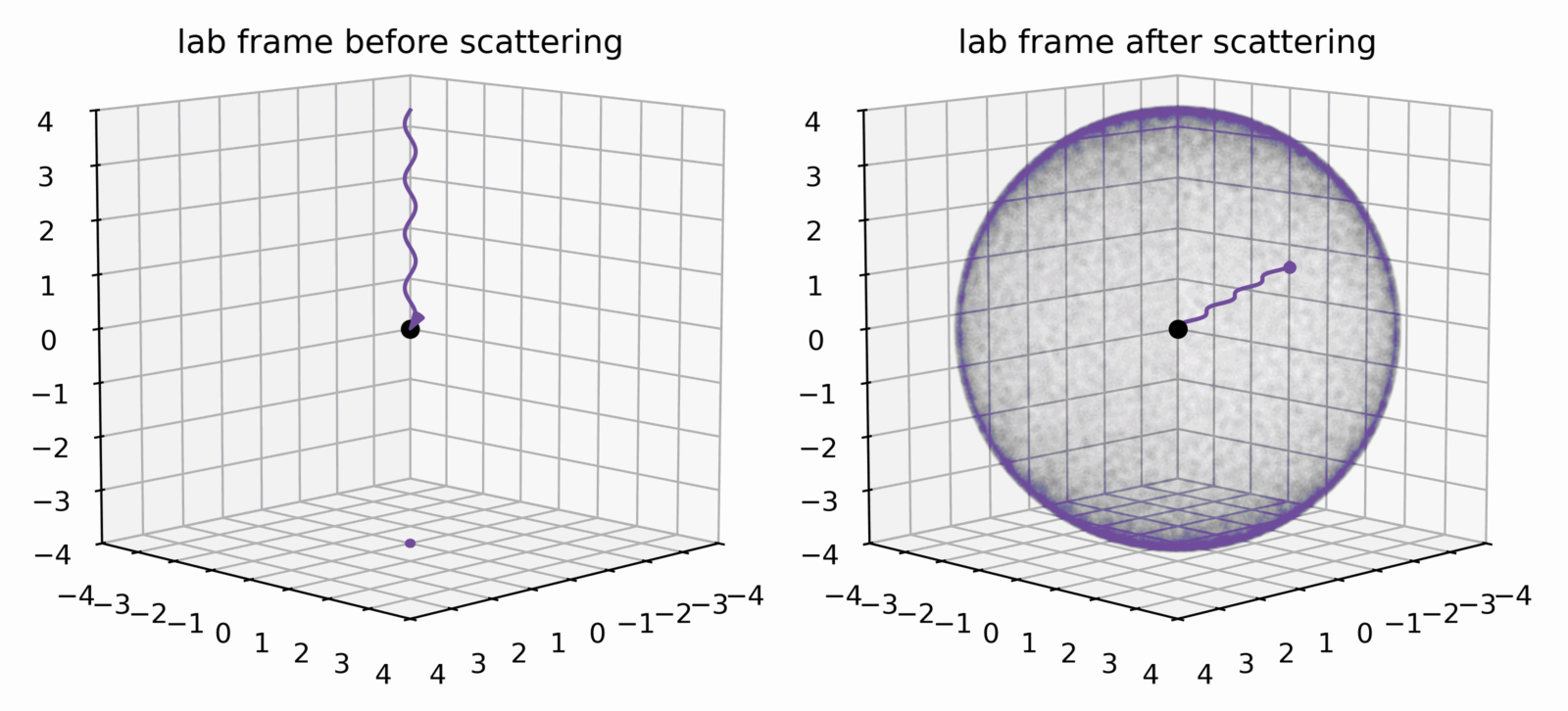
So, light can scatter off an electron, but so far, no energy has been exchanged between the two scattering partners, and this is where Arthur Holly Compton comes enters the story.
Compton scattering
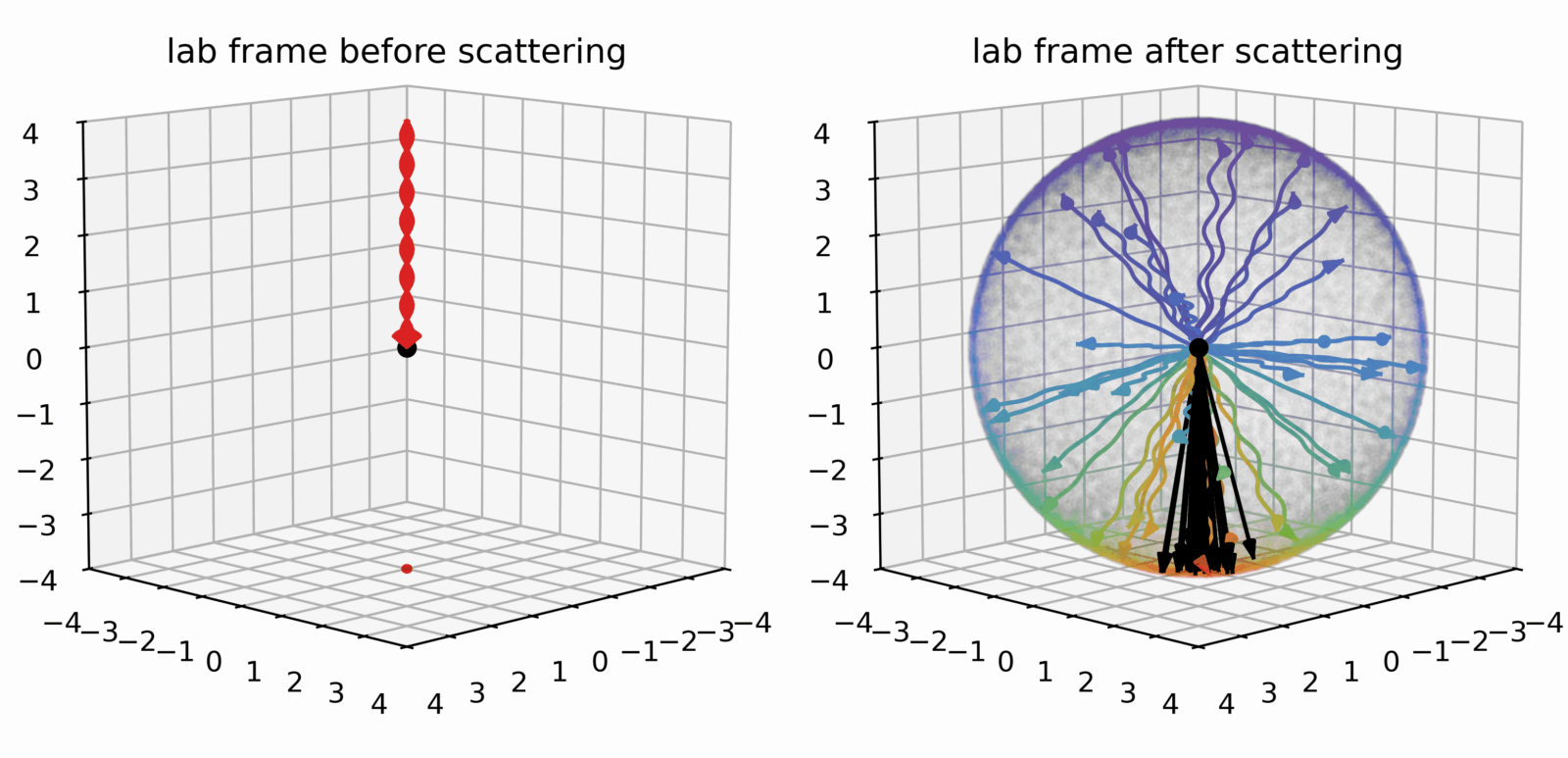
In the Thomson scattering case, the purple color represents the photon energy, which does not change notably by a scattering event. However, in his famous experiment in 1923, Arthur Holly Compton scattered X-rays, i.e. light or photons of about 10000x higher energies than optical light, on electrons approximately at rest. In contrast to Thomson’s theory for low-energy optical light, he found that the X-ray photons transferred a measurable amount of energy to the electron depending on the scattering angle. This is illustrated in Fig. 2, for a large number of photons (red waves in the left panel) all coming in from the same direction (pointing towards the red dot at the bottom) and scattering on the electron at rest (central black dot). The right panel shows then that after scattering these photons change their energy depending on the scattering angle, from red (initial high energy) via yellow, green, blue to purple (low energy). While the purple back-scattered region corresponds to a large energy transfer to the electron, the forward scattering corresponds to only a “light touch” with the original photon passing by almost unaffected. So, Compton found that when the photon energy becomes large enough, it can also transfer energy to the electron (see also the black arrows visualizing the direction of the electron momentum after the scattering, although not scaled). But didn’t we want to understand how the photon gains energy from electron?
Before understanding this inverted Compton scattering, we first need to complete the quantum picture of photon-electron billiards with one more puzzle piece concerning the cross section. As in Fig. 1, the sphere of dots shows also for the Compton regime that the probability of scattering follows the same, almost uniform distribution as for the Thomson case. But when increasing the energy of the light from X-rays to even higher-energetic gamma-rays, also Compton’s theory is not enough, and the Klein-Nishina modification becomes relevant.
Klein-Nishina regime
After Compton’s groundbreaking experiments, it was however noted that the uniform Thomson scattering sphere from Fig. 2 was deviating from the observations of light at even higher energies. In 1928, the two theoretical physicists Oskar Klein and Yoshio Nishina resolved this conflict by using a freshly developed quantum-field-theoretical approach, that combined the existing non-relativistic quantum theory with the principles of special relativity. Within this new framework, they derived the missing factor in the Thomson/Compton theory that matches observations well until even today’s precision measurements at modern particle colliders. The key change occurs when the photon energy becomes similar or greater to the rest mass energy of the electron. This rest mass energy is universally constant and defined by Einstein’s famous relation E=mc², with the particle mass and c is the speed of light. This makes intuitively sense: In the Thomson limit, the momentum of the photon is negligible compared to the “heavy” electron (think of a ping-pong ball hitting a billiards ball), whereas in the Klein-Nishina regime the photon carries such large momentum that the electron is mass is “very light” (think of a billiard ball hitting a ping-pong ball). In the Klein-Nishina regime as shown in Fig. 3, it becomes then much less favorable to scatter into the backward direction, in which case the energy transfer is very large (from initially red to purple). Instead, most of the scattering happens in the forward direction, with again only a small exchange of energy.
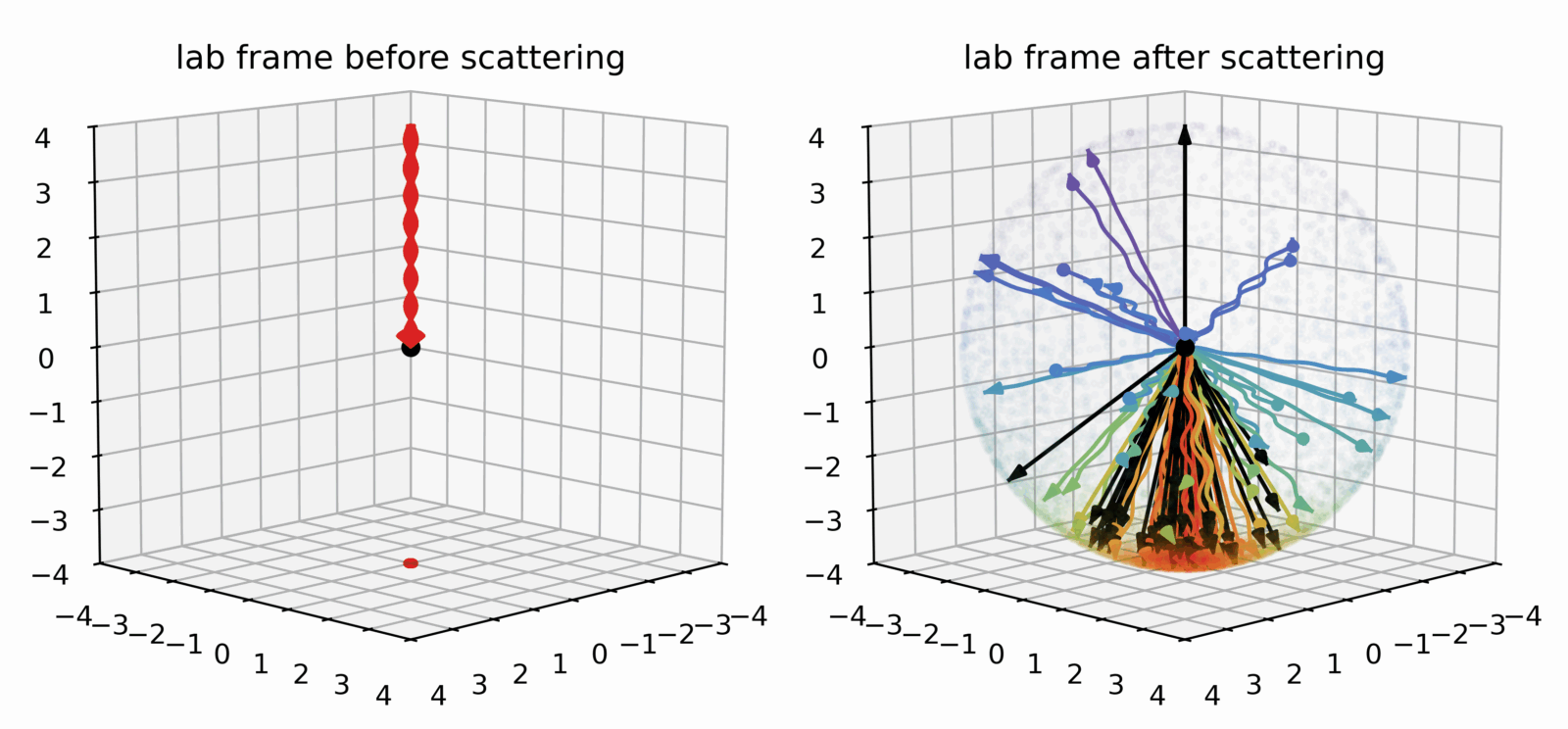
With this, we have completed the first part of the blog: Light waves or photons do scatter of electrons, which is generally covered under the name of Compton scattering. When we place the electron at rest, and let a photon scatter on it, two regimes occur, depending on the energy of the incoming photon: If the energy is small compared to the rest mass energy of the electron, the scattering is basically elastic, i.e. no energy is exchanged, and the outgoing direction is almost isotropically distributed, i.e. scattering happens in all directions almost equally likely. The electron is a strong bouncer and won’t let the photon pass through. This situation changes dramatically, when the photon energy is larger than the electron rest mass energy. Then it is the photon rushing through, bouncing less likely and mainly only into the photon direction, and transferring some of its energy to the electron.
In part 2, we will put this picture together with relativistic electrons, i.e. moving almost at the speed of light, in which case the energy transfer can effectively inverted to eventually understand the origin of the ultra-high-energy photons.



