Semi-analytical models — hydrodynamical “backbone”
One area where our group is active is on building a better theoretical picture of how jets form and are launched from black holes in general, and their internal workings.
Accreting black holes are complex systems, so there are naturally limitations –both technological and in our current physical understanding — to the level of detail that can be included in any model. Addressing and overcoming these limitations to obtain a more complete view of black hole accretion and jet formation is a key theme of our group’s research activities.
There are generally two approaches to such models: semi-analytical, where we make many simplifying assumptions so that we can build a toy model of the jet dynamical structure, within which we can solve the full equations leading to radiation and thus compare our models with multi-wavelength data. Alternately, we can use sophisticated simulations where the evolution in the physics of individual plasma cells is followed exactly, but at such high cost in terms of computational power (CPU) that only limited parts of the system can be explored. Our group is involved in both approaches, with the hope that by tackling different aspects of the same systems, we can derive answers to some long-standing problems.
On the semi-analytical front, we have done significant work over the years in modeling the broadband (radio through X-ray and γ-ray) spectra of the steady, compact jets associated with weakly accretion AGN and “hard state” BHBs. The original model simplified the jet dynamics by assuming a freely-expanding hydrodynamical (HD) plasma only (ie., the magnetic field is kept as a global property but not included in the dynamical equations), based on work in Falcke (1996) and Falcke & Biermann (1999). The jet is assumed to expand laterally with the local sound speed (cs), creating a pressure gradient that accelerates the plasma along the jet axis up to Lorentz factors of ~2-3. While we know that ignoring the roll of the field in the derivation of the velocity gradient is an omission, the resulting velocity of profile is quite similar to what results from including the magnetic field (we now know from more recent work; Polko et al. 2010, 2011). Once the velocity profile is defined, and initial conditions set at the base of the jets (allowing us to test various scenarios for these configurations against the data), conservation laws determine the profiles of parameters like density and magnetic field strength along the jets. One other simplification is the treatment of particle distributions, because observations indicate the presence of acceleration of particles from assumedly thermalized distributions to power-laws, usually assumed to occur via turbulent shocks. Because this process is very complex and the topic of entire simulations elsewhere, we approximate this by (usually) assuming that particles enter the jet from the accretion flow in a thermal distribution, and at a distinct location (which we fit for from the data) a fraction of the particles are accelerated into a power-law tail. At this stage we can calculate the expected emission from various processes like synchrotron emission and inverse Compton scattering, as well as include other components like thermal disk and stellar emission. All of these emission processes combine to form a composite spectral energy distribution (SED), as shown in schematic in the figure below.
This class of models has been successful at fitting data from both nearby low luminosity AGN such as Sgr A* and M81, as well as a host of Galactic BHBs (see, e.g., Markoff et al. 2001ab, Markoff et al. 2005, Migliari et al. 2007, Gallo et al. 2007, Maitra et al. 2009).
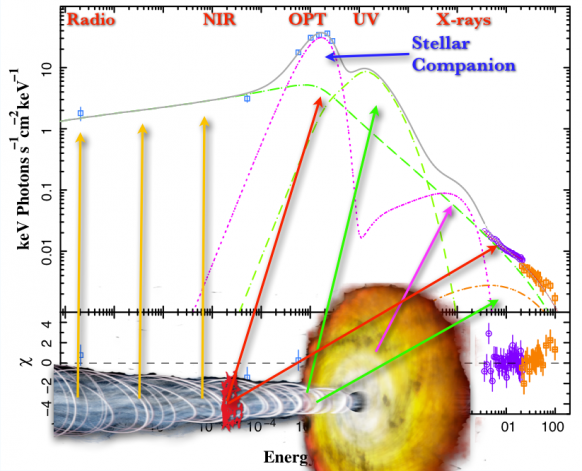
Semi-analytical models — MHD “backbone” + Particle Acceleration
While successful at capturing several important elements of jet physics (see, e.g., Fundamental Plane below), the exclusion of the magnetic field has hampered our ability to test scenarios based on magnetohydrodynamical (MHD) simulations performed by ourselves and others, and is not self-consistent. In more recent work we have derived a new dynamical jet model based on the full MHD prescription, using some tricks to simplify the mathematics by assuming self-similarity in the shape of the magnetic field lines (see Vlahakis & Königl 2003). This assumption is well justified based on the outcomes of simulations, where the jets are very laminar in the regions we are interested in:

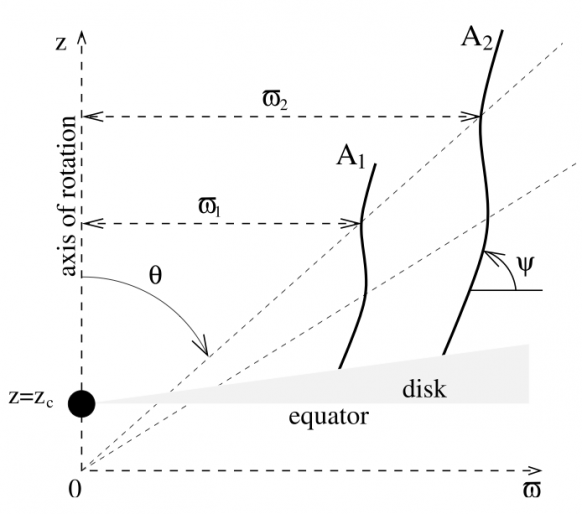
In a series of papers (Polko et al. 2010, Polko et al. 2011, Polko et al. in prep.) we have found a new set of relativistic jet solutions for a hot plasma and including gravity, that maintains self-similarity in the regime of interest, and which crosses all three critical points of an MHD flow: the modified magnetosonic slow point (MSP), the Alfvén point (AP) and the modified magnetosonic fast point (MSP). The MSP is the point we associate with the launch point/nozzle of the jets, and conditions there can be matched to accretion flow solutions. Using these boundary conditions, a flow solution can be derived which self-consistently determines the jet dynamical profile as well as the location of the MFP. The MFP is an important flow point, beyond which the flow is out of causal contact with the downstream plasma, thus allowing instabilities and disruptions to form shocks (in our calculations this region is associated with recollimation shocks for instance). We associate the MFP with the start of particle acceleration processes, which before we treated as a free parameter. Now this location is derived consistently within the MHD framework, and conditions at the accretion flow determine a unique solution for the outer flow, linking the inflow to particle acceleration for the first time. We are in the process of solving these equations for a variety of systems and forming a new grid-based model.
Time Dependence
Both the HD and MHD frameworks above assume a steady state jet, for simplicity, because these states are extended in both AGN and BHBs. However in order to model state transitions, time dependence must be incorporated. We are currently working on several aspects of this problem (Maitra et al. 2009, Pe’er & Markoff in prep.).
Hadronic components and high-energy particle production
The matter content of jets is still unknown. Theoretically many groups favor leptonic models, where most of the plasma is dominated by electron-positron pairs. Such a scenario would result if the jets were mainly loaded via pairs created in strong magnetic fields at the base of the jets. These types of jets are what generally appear in MHD simulations, but it is important to note that there are numerical (code) reasons why mass is not loaded onto the jets from the accretion flow, which certainly contains hadrons! Hadrons are also present in at least some jets at larger distances, because we detect high-energy cosmic rays that are too energetic to come from anything other than AGN jets or extreme events like gamma-ray bursts (GRBs). It is a major question right now in the field whether the hadrons are loaded from the start or entrained later into a predominantly pair-dominated jet.
The presence of hadrons will affect the spectrum. To address the question of matter content explicitly, we are developing a new model that includes hadron acceleration and its secondary particle production via internal collisions. From this new model we will be able to discern purely leptonic from hadronic jets by comparing the observed to the modeled spectrum. While many groups are active, our focus on also explaining trends from the “low” energy (radio-IR) as well as mass-scaling physics is distinct.
Comparison of BHBs to NSBs
BHBs and NSBs are both powered by accretion onto a compact object, and there are many similarities between the two classes of objects. However, there are also major differences. For example, NSs are less massive than BHs (2-3 times the mass of the Sun vs. ~10 times the mass of the Sun). Also, NSs have a surface that can radiate (while BHs do not), NSs have stronger magnetic fields and more energetic accretion disks, and NSBs emit less radiation in the radio band compared to BHBs. The jet model described above has been very successful at modeling BHBs, at we are investigating how differences in fits to NSBs can help us pinpoint where the physics diverges for these two source classes.
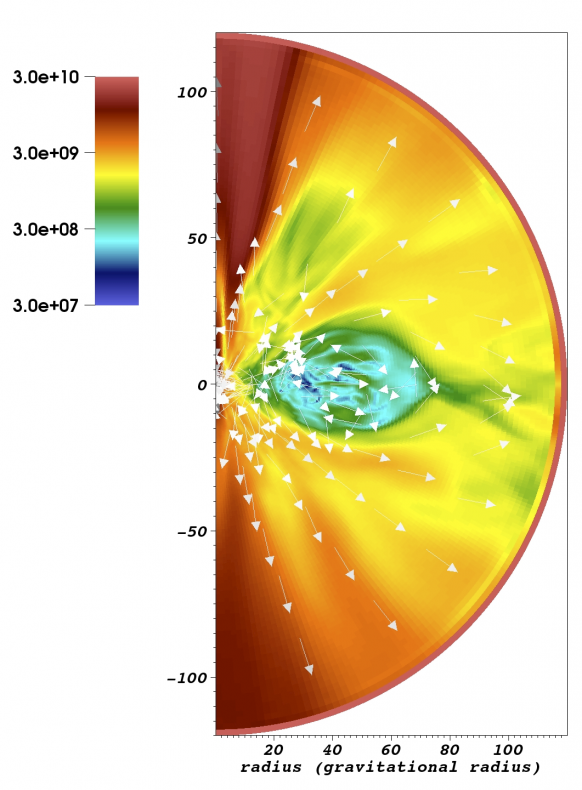
MHD Simulations of the Accretion Flow
In collaboration with Chris Fragile (College of Charleston, USA) we are using the fully general relativistic MHD code COSMOS++, because of its unique capability in accounting for radiative cooling in the optically thin regime. By including cooling self-consistenly, we are able to produce spectral energy distributions from these simulations and directly compare them to data. Our attention is currently focused on the SMBH lurking at the center of our Galaxy: Sgr A*, which is about 4 million times more massive than our Sun. We set physical conditions within the simulation to match Sgr A*’s extraordinarily low accretion rate, and then have developed a post-processing routine for calculating the SED, using GR ray tracing with the help of collaborator Jason Dexter. (Dibi, Drappeau, Fragile & Markoff, in prep.; Drappeau, Dibi, Dexter, Markoff & Fragile, in prep.).
Comparison of BHBs and AGN
One very interesting possibility is that the accretion states in BHBs may have longer lived analogs in AGN, in other words, some classes of AGN may in fact be temporal states of similar objects. Our group is at the forefront of studies comparing XRB and AGN accretion physics, having discovered, along with collaborators, the Fundamental Plane of black hole accretion, and working on new techniques to test the extent to which mass scaling can be applied to understand how XRB states extend to AGN zoology.
